回形数组的自我解答

发表于 更新于 分类于 ， 阅读次数： Waline： 本文字数： 1.9k 阅读时长 ≈ 2 分钟

  在对java基础进行查漏补缺时，在尚硅谷的视频里，老师提到这个面试题。他说那个孩子坐下十多分钟没做出来就走了。来很久，回也很久。

  我也想试试，坐在电脑前想，最后发现还是要纸。

  偷偷告诉你：这是我没查答案做出来的，真是太棒了。

前期想法

  由于当时老师刚讲完杨辉三角，而我做杨辉三角是不用数组进行存储的，而是用组合数直接算，直接打印，想算多少算多少。因此我的初步想法是直接打印，与此对应的思路是两个for，通过判断对i和j进行操作，以进行旋转。此时还是正着走的。

  因为暂时想不出，就使用纸张进行画图。最先发现的是奇偶的最后的拐弯不一样。于是又算出最后一个数的坐标。阿巴阿巴阿巴（省略一大段）。

最终想法

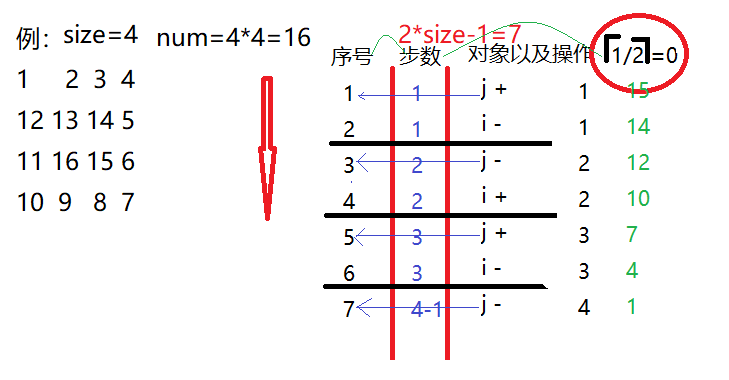
  一言以蔽之，倒着走，算出拐弯，算出步数以及操作方式和操作对象。

  虽然中间思考很久，但我不想叨逼叨这些碎碎念。

回旋数组的解题思路以例4.png

代码

  这是用Sublime写的，不想打开idea。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
java.util.Scanner scancer = new java.util.Scanner(System.in);
	int size = scancer.nextInt();//要大于1
	int num = size * size;
	int i,j;
	/**
	旋转数矩阵
	思路：根据矩阵大小算出最后一个数并算出它的位置，
	通过观察发现，倒着旋转，奇数和偶数的矩阵里最后的旋转不同（即不是i，就是j）。
	通过矩阵大小，算出拐弯次数。
	倒着看，算出每走（size=4为例，1，1，2，2，3，3，3（4跳出成3））拐弯。
	倒着看，每次拐弯后对i，j的操作不同，两两一组，根据第几次循环判断对i还是j操作，根据每两次（根据次数算出第几组，根据组确定操作是+还是-）
	*/
	int[][] mat = new int[size][size];
	/*分奇偶情况*/
	if (size % 2 == 0) {
		/*顺着数，最后一个数*/
		j = (i=size/2) - 1;
		mat[i][j] = num;
		/*控制循环次数，也可理解为共拐几次弯。例：size=4，共拐2*size-1次弯*/
		label:for (int l = 1; l < 2*size ; l++ ) {
			/*第几组，和 走多少步后拐弯*/
			int temp = (int)java.lang.Math.ceil((float)l/(float)2);//注意如果不强转的话，最后一行只有一个。因为1/2=0，而我不能要0，要从1开始。
			for (int m = 0;m < temp;m++ ) {
				if(l % 2 == 1){//j 更改1为0可实现顺时针旋转
					if (temp % 2 == 1) {
						/*右移*/
						j+=1;
					}else{
						/*左移*/
						j-=1;
					}
				}else{//i
					if (temp % 2 == 1) {
						/*上移*/
						i-=1;
					}else{
						/*下移*/
						i+=1;
					}
				}
				
				mat[i][j] = (num-=1);
				if (1 == num) {
					/*这里就是最后一组的第一个的最后要少走一步（即最后一次拐弯后，最后一步）*/
					break label;
				}
			}
	}
	}else{
		i = j = size / 2;
		mat[i][j] = num;
	label:for (int l = 1; l < 2*size ; l++ ) {
			int temp = (int)java.lang.Math.ceil((float)l/(float)2);
			for (int m = 0;m < temp;m++ ) {
				
				if(l % 2 == 1){//j
					if (temp % 2 == 1) {
						j-=1;
					}else{
						j+=1;
					}
				}else{//i
					if (temp % 2 == 1) {
						i+=1;
					}else{
						i-=1;
					}
				}
				mat[i][j] = (num-=1);
				if (1 == num) {
					break label;
				}
			}
	}
	}
	for (int l = 0; l <mat.length ; l++ ) {
		for (int m = 0; m < mat[l].length; m++ ) {//这里也可以顺时针旋转
			System.out.print(mat[l][m]+"\t");
		}
		System.out.println();
	}

思考

  对于当时弹幕里的对角线，我暂时没想出。对于我这个代码，感觉可以奇偶合并在一起。我的想法是，构造一个函数对操作对象和操作方式进行映射。